Generalized viscoelastic wave equation

Wang, Yanghua

doi:10.1093/gji/ggv514

Abstract

This paper presents a generalized wave equation which unifies viscoelastic and pure elastic cases into a single wave equation. In the generalized wave equation, the degree of viscoelasticity varies between zero and unity, and is defined by a controlling parameter. When this viscoelastic controlling parameter equals to 0, the viscous property vanishes and the generalized wave equation becomes a pure elastic wave equation. When this viscoelastic controlling parameter equals to 1, it is the Stokes equation made up of a stack of pure elastic and Newtonian viscous models. Given this generalized wave equation, an analytical solution is derived explicitly in terms of the attenuation and the velocity dispersion. It is proved that, for any given value of the viscoelastic controlling parameter, the attenuation component of this generalized wave equation perfectly satisfies the power laws of frequency. Since the power laws are the fundamental characteristics in physical observations, this generalized wave equation can well represent seismic wave propagation through subsurface media.

Non-linear differential equation, Seismic attenuation, Wave propagation

INTRODUCTION

For seismic wave simulation, there are two basic types of wave equations: pure elastic wave equation and viscoelastic wave equation. This paper proposes to unify these two types of wave equations into a single wave equation.

The seismic property of subsurface media should generally be considered to be a superposition of Hook's pure elastic model and a viscoelastic model. Customarily, the Kelvin–Voigt model assumes the seismic property to be a stack of the elastic model and a Newtonian viscous model. The latter is a linear viscosity in which the stress–strain relationship is presented by a first-order temporal derivative. Thus, the Kelvin–Voigt model is given as the following:

\begin{equation} \sigma (t) = {E_0}\varepsilon (t) + {E_1} \frac{{{\rm d}\varepsilon (t)}}{{{\rm d}t}}, \end{equation}

(1)

where σ(t) is the time-dependent tensile stress, ε(t) is the corresponding strain and E₀ and E₁ are two parameters of the model. In eq. (1), E₀ε is the elastic term and E₁dε/dt is the linear viscous term. This leads to a well-known wave equation called the Stokes equation.

However, subsurface media behave in a much generalized viscoelastic manner. To reflect this characteristic, a stress–strain relationship can be described by a fractional order, instead of the first order, temporal derivative. Then, the superposition model can be expressed as

\begin{equation} \sigma (t) = {E_0}\varepsilon (t) + {E_1} \frac{{{{\rm d}^\beta }\varepsilon (t)}}{{{\rm d}{t^\beta }}}, \end{equation}

(2)

where β is the fractional order of the time differential. The last term E₁d^βε/dt^β uses a compact form of fractional derivative to describe the frequency and time dependency of a viscoelastic system (Scott-Blair 1947).

The mathematical-physics history of this empirical method, using a fractional derivative to represent the viscoelastic property, begins with Nutting (1921) who reported the observation that the stress relaxation could be modelled by fractional powers of time. Such a model is in sharp contrast to the traditional view that stress relaxation is best described by decaying exponentials. Gemant (1936) further observed that the stiffness and damping properties of viscoelastic materials appeared to be proportional to fractional powers of frequency. Scott-Blair (1947) pioneered a framework which used fractional order temporal derivatives to model simultaneously the observations of Nutting (1921) and Gemant (1936). Then, Caputo (1966, 1967) used the fractional order derivatives to model the viscoelastic behaviour of the earth's subsurface media.

Eq. (2) is identical to or almost identical to, respectively, all of the fractional calculus relationships reported in the literature (Caputo 1967; Caputo & Mainardi 1971; Bagley & Torvik 1983; Szabo 1994; Mainardi & Tomirotti 1997; Wismer 2006; Holm & Sinkus 2010; Jaishankar & McKinley 2013; Näsholm & Holm 2013). When the fraction β equals to 1, eq. (2) reduces to eq. (1), in which the viscoelastic model becomes Newtonian viscous model (Ricker 1943). However, when the fraction β equals to 0 and the viscosity is zero-valued, eq. (2) becomes σ(t) = (E₀ + E₁)ε(t), which is not the pure elastic model. Because eq. (2) cannot represent the pure elastic case, then the derived wave equation lacks generality for seismic waves.

This paper attempts to unify the viscoelastic and pure elastic cases into a single model. In this unified model, β still varies between 0 and 1. But, when the fraction β equals to 0, the model is able to represent any pure elastic media. The unified model leads to a generalized wave equation, for which an analytical solution is derived explicitly in terms of the attenuation and velocity dispersion. Moreover, this paper proves that the attenuation component of the unified wave equation follows power laws. The power-law attenuation is a fundamental characteristic, observed from many measurements and is reported in the vast body of the published literature. Therefore, this generalized wave equation can perfectly represent seismic wave propagation through subsurface media.

GENERALIZED WAVE EQUATION

This section unifies wave equations for the pure elastic and viscoelastic cases into a single wave equation.

Unified elastic-viscoelastic model

For an ideal elastic solid, according to Hooke's law, there is a linear relationship between stress and strain:

\begin{equation} \sigma (t) = E\varepsilon (t), \end{equation}

(3)

where E is Young's modulus. For an ideal viscous fluid, there is a linear relationship between the stress and the strain rate:

\begin{equation} \sigma (t) = \eta \frac{{{\rm d}\varepsilon (t)}}{{{\rm d}t}}, \end{equation}

(4)

where η is the viscosity coefficient. This is Newton's fluid law.

To describe the viscoelastic characteristic of a solid material, Newton's fluid law should be modified. It is logical to think that the viscoelasticity should behave in the intermediate state between the pure Hookean elastic solid and the pure Newtonian fluid:

\begin{equation} \sigma (t) = {E^{1 - \beta }}{\eta ^\beta } \frac{{{{\rm d}^\beta }\varepsilon (t)}}{{{\rm d}{t^\beta }}}, \end{equation}

(5)

where β is an interpolation coefficient, set between 0 and 1. When β = 0, it is Hooke's law. When β = 1, it is Newton's fluid law. Thus, eq. (5) is an intermediate, viscoelastic model (Scott-Blair 1947; Smit & de Vries 1970), in which the stress is related to a fractional strain rate. For a comprehensive review of fractional viscoelastic models, readers may refer to Mainardi (2010).

The subsurface media should have a behaviour that combines the pure elastic characteristic (eq. 3) and the viscoelastic characteristic (eq. 5). Therefore, we may set a constitutive stress–strain equation as the following:

\begin{equation} \sigma (t) = E\left( {\varepsilon (t) + \beta {\tau ^\beta } \frac{{{{\rm d}^\beta }\varepsilon (t)}}{{{\rm d}{t^\beta }}}} \right), \end{equation}

(6)

where τ = η/E, which is referred to as the retardation time.

In this constitutive equation, for the unified elastic-viscoelastic model, the β factor pre-multiplied to the viscoelastic term is a combining factor in order to balance the elastic and the viscoelastic characteristics. We introduce the combining factor β here to ensure that eq. (6) is a pure elastic model when β = 0 and a linear viscoelastic model when β = 1.

The combining factor

If denoting the combining factor by q, eq. (6) is a case with q = β. A more general form can be expressed as

\begin{equation} \sigma (t) = E\left( {\varepsilon (t) + q{\tau ^\beta }\frac{{{{\rm d}^\beta }\varepsilon (t)}}{{{\rm d}{t^\beta }}}} \right). \end{equation}

(7)

If q = 1, eq. (7) is the conventional viscoelastic model (2).

In the frequency domain, the module of eq. (7) is

\begin{equation} \left| {\sigma (\omega )} \right| = f(\beta ,q)\left| {E\varepsilon (\omega )} \right|, \end{equation}

(8)

where f(β, q) is a square root coefficient:

\begin{equation} f(\beta ,q) = \sqrt {1 + 2q\frac{{{\omega ^\beta }}}{{\omega _0^\beta }} \cos \frac{{\beta \pi }}{2} + {q^2}\frac{{{\omega ^{2\beta }}}}{{\omega _0^{2\beta }}}} , \end{equation}

(9)

with ω₀ ≡ τ^{− 1}.

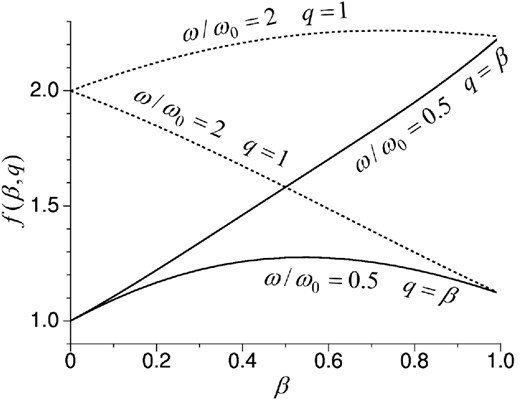
Fig. 1 illustrates this f(β, q) coefficient in two cases: q = β (solid curves) and q = 1 (dotted curves). Each case displays two numerical examples with ω/ω₀ = 0.5 and 2, respectively. In the case where q = β (the solid curves), eq. (6) approaches the pure elastic model, |σ(ω)| = |Eε(ω)|, when β → 0. However, for the case of q = 1 (the dotted curves), which is the commonly used case, eq. (7) approaches |σ(ω)| = 2|Eε(ω)| when β → 0. The latter is not the Hookean elastic model.

Figure 1.

Open in new tab Download slide

The square root coefficient f(β) in the viscoelastic model: comparison between the case with the combining factor q = β (solid curves) and the case q = 1 (dotted curves). Each case displays two numerical examples with ω/ω₀ = 0.5 and 2, respectively.

For generality, the combining factor q can be set as a β-dependent function, such as q = β^a, where a is a non-zero value. We have tested q = β^1/2 and q = β² (results not shown) and found that q = β is the best for balancing the elasticity and the viscosity in the model.

The wave equation

To describe wave motion, Newton's second law should always be used. Following the principle of momentum conservation, Newton's second law is formulated as

\begin{equation} \nabla \sigma (t) = \rho \frac{{{{\rm d}^2}u(t)}}{{{\rm d}{t^2}}}, \end{equation}

(10)

where u(t) is the displacement. Eliminating the stress in Newton's second law (10), by substituting stress σ(t) by the fractional constitutive eq. (6) and replacing strain ε(t) with the gradient of the displacement, ε(t) = ∇u(t), the viscoelastic wave equation may be formed as

\begin{equation} {\nabla ^2} \left( {1 + \beta {\tau ^\beta }\frac{{{{\rm d}^\beta }}}{{{\rm d}{t^\beta }}}} \right) u(t) - \frac{1}{{{c^2}}}\frac{{{{\rm d}^2}u(t)}}{{{\rm d}{t^2}}} = 0, \end{equation}

(11)

where |$c = \sqrt {E/\rho }$|⁠. This wave equation contains fractional derivatives, with respect to time, in addition to the second-order temporal and spatial derivatives. It is a general wave equation, being valid for either the pure elastic case or the viscoelastic case.

Although various constitutive viscoelastic equations may lead to different forms of wave equation (Holm & Näsholm 2014), the combination between the elastic model and the viscoelastic model should be the same as proposed in this paper.

THE ANALYTICAL SOLUTION

This section derives explicitly an analytical solution to the generalized wave equation.

In the case of plane waves moving along the x-axis, the viscoelastic wave equation is

\begin{equation} \left[ {\frac{{{\partial ^2}}}{{\partial {x^2}}}\left( {1 + \beta {{\left( {{\rm i}\frac{\omega }{{{\omega _0}}}} \right)}^\beta }} \right) + \frac{{{\omega ^2}}}{{{c^2}}}} \right]u(\omega ) = 0, \end{equation}

(12)

where ω₀ ≡ τ^{− 1}. The wave solution can be given in the form of

\begin{equation} u(\omega ) = {u_0}\exp \left( { - \alpha (\omega )x - {\rm i}\frac{{\omega x}}{{v(\omega )}}} \right), \end{equation}

(13)

where α(ω) is the attenuation and v(ω) is the phase velocity. Eq. (12) can be written as

\begin{equation} (1 + {{\rm i}^\beta }Q)\left( {{\alpha ^2} + {\rm i}2\alpha \frac{\omega }{v} - \frac{{{\omega ^2}}}{{{v^2}}}} \right) + \frac{{{\omega ^2}}}{{{c^2}}} = 0, \end{equation}

(14)

where |$Q = \beta {\omega ^\beta }/\omega _0^\beta$| and |${{\rm i}^{\,\beta} } = \cos {{{\beta \pi } \over 2}} + {\rm i}\sin {{{\beta \pi } \over 2}}$|⁠. This leads to two simultaneous equations,

\begin{equation} \left\{ \begin{array}{@{}l@{}} \left( {1 + Q\cos \frac{{\beta \pi }}{2}} \right) \left( {{\alpha ^2} - \frac{{{\omega ^2}}}{{{v^2}}}} \right) - 2\alpha \frac{\omega }{v}Q\sin \frac{{\beta \pi }}{2} + \frac{{{\omega ^2}}}{{{c^2}}} = 0,\\ Q\sin \frac{{\beta \pi }}{2}\left( {{\alpha ^2} - \frac{{{\omega ^2}}}{{{v^2}}}} \right) + 2\alpha \frac{\omega }{v}\left( {1 + Q\cos \frac{{\beta \pi }}{2}} \right) = 0. \end{array} \right. \end{equation}

(15)

Because |$1 + Q\cos {{{\beta \pi } \over 2}} > 0$|⁠, for 0 ≤ β ≤ 1, the second equation can be rewritten as

\begin{equation} 2\alpha \frac{\omega }{v} = - Q\sin \frac{{\beta \pi }}{2}\left( {{\alpha ^2} - \frac{{{\omega ^2}}}{{{v^2}}}} \right){\left( {1 + Q\cos \frac{{\beta \pi }}{2}} \right)^{ - 1}}. \end{equation}

(16)

Substituting this expression into the first equation of (15) produces

\begin{equation} \frac{\omega }{v} = \sqrt {{\alpha ^2} + \frac{{{\omega ^2}}}{{{c^2}}}\frac{{1 + Q\cos {{{\beta \pi } \over 2}}}}{{1 + 2Q\cos {{{\beta \pi } \over 2}} + {Q^2}}}} . \end{equation}

(17)

Substituting (17) into the second equation of eq. (15) leads to

\begin{eqnarray} {\alpha ^4} &+& {\alpha ^2}\frac{{{\omega ^2}}}{{{c^2}}}\frac{{1 + Q\cos {{{\beta \pi } \over 2}}}}{{1 + 2Q\cos {{{\beta \pi } \over 2}} + {Q^2}}}\nonumber\\ &-& \frac{1}{4}\frac{{{\omega ^4}}}{{{c^4}}}\frac{{{Q^2}{{\sin }^2}{{{\beta \pi } \over 2}}}}{{{{\left( {1 + 2Q\cos {{{\beta \pi } \over 2}} + {Q^2}} \right)}^2}}} = 0, \end{eqnarray}

(18)

in which |$1 + 2Q\cos {{{\beta \pi } \over 2}} + {Q^2} > 0$| is always satisfied. Solving this equation can find the attenuation:

\begin{eqnarray} \alpha = \frac{\omega }{{c\sqrt 2 }}\sqrt {\frac{1}{{\sqrt {1 + 2Q\cos {{{\beta \pi } \over 2}} + {Q^2}} }} - \frac{{1 + Q\cos {{{\beta \pi } \over 2}}}}{{1 + 2Q\cos {{{\beta \pi } \over 2}} + {Q^2}}}} .\nonumber\\ \end{eqnarray}

(19)

Substituting eq. (19) into eq. (17) produces the solution for velocity dispersion:

\begin{eqnarray} \frac{\omega }{v} = \frac{\omega }{{c\sqrt 2 }}\sqrt {\frac{1}{{\sqrt {1 + 2Q\cos {{{\beta \pi } \over 2}} + {Q^2}} }} + \frac{{1 + Q\cos {{{\beta \pi } \over 2}}}}{{1 + 2Q\cos {{{\beta \pi } \over 2}} + {Q^2}}}} .\nonumber\\ \end{eqnarray}

(20)

Inserting |$Q = \beta {\omega ^\beta }/\omega _0^\beta$| back into eqs (19) and (20), the analytical expressions for α(ω) and v(ω) are

\begin{equation} \alpha = \frac{\omega }{c}\sqrt {\frac{{A - B}}{2}} , \end{equation}

(21)

\begin{equation} \frac{\omega }{v} = \frac{\omega }{c}\sqrt {\frac{{A + B}}{2}} , \end{equation}

(22)

respectively, where

\begin{eqnarray} A &=& {{\left( {1 + 2\beta \frac{{{\omega ^\beta }}}{{\omega _0^\beta }}\cos \frac{{\beta \pi }}{2} + {\beta ^2}\frac{{{\omega ^{2\beta }}}}{{\omega _0^{2\beta }}}} \right)}^{ - 1/2}},\nonumber\\ B &=& \left( {1 + \beta \frac{{{\omega ^\beta }}}{{\omega _0^\beta }}\cos \frac{{\beta \pi }}{2}} \right){A^2}. \end{eqnarray}

(23)

Fig. 2 displays the attenuation and the dispersion functions versus various β values. The horizontal axis (ω/ω₀) is the normalized frequency. For the attenuation, the vertical axis ((ω₀/c)^{− 1}α) is a scaled attenuation, in which the scalar (ω₀/c)^{− 1} has physical units of distance. For the velocity dispersion, the vertical axis (v(ω)/c) is a normalized phase velocity.

Figure 2.

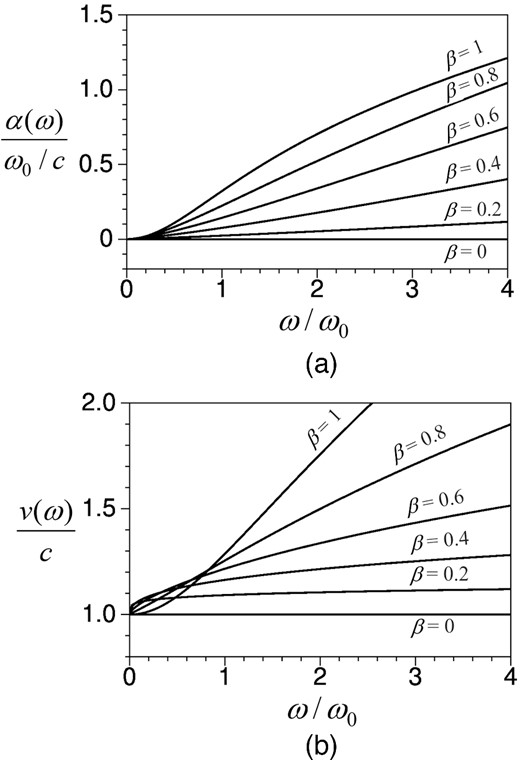
(a) The attenuation versus the β values. The horizontal axis (ω/ω0) is normalized frequency and the vertical axis is the attenuation α(ω) normalized by ω0/c, which has physical units of inverse distance. (b) Velocity dispersion versus the β values. The vertical axis is the phase velocity v(ω) normalized by the velocity c.

Open in new tab Download slide

(a) The attenuation versus the β values. The horizontal axis (ω/ω₀) is normalized frequency and the vertical axis is the attenuation α(ω) normalized by ω₀/c, which has physical units of inverse distance. (b) Velocity dispersion versus the β values. The vertical axis is the phase velocity v(ω) normalized by the velocity c.

In the case of β = 1, the linear viscosity, then

\begin{eqnarray} A &=& {{\left( {1 + \frac{{{\omega ^2}}}{{\omega _0^2}}} \right)}^{ - 1/2}} = \cos 2\theta ,\nonumber\\ B &=& {{\left( {1 + \frac{{{\omega ^2}}}{{\omega _0^2}}} \right)}^{ - 1}} = {{\cos }^2}2\theta , \end{eqnarray}

(24)

where (ω/ω₀)² = tan 2θ is denoted. The attenuation and velocity dispersion can be expressed as

\begin{eqnarray} \alpha &=& \frac{\omega }{c}\sqrt {\cos 2\theta } \sin \theta ,\nonumber\\ \frac{\omega }{v} &=& \frac{\omega }{c}\sqrt {\cos 2\theta } \cos \theta . \end{eqnarray}

(25)

These are the analytical solutions presented in Ricker (1943).

If β = 0, it is easy to verify that α(ω) = 0 and v(ω) = c. This is a pure elastic case. However, for the conventional equation in the previous body of literature, where the combining factor is q = 1, rather than q = β in eq. (11), eq. (22) will lead to v(ω) ≠ c when β = 0. This emphasizes the necessity of the combining factor β introduced in wave equation (11).

POWER LAWS FOR THE ATTENUATION

A fundamental characteristic of the viscoelastic media is that the attenuation satisfies power laws of frequency, for both compressional and shear waves (Collins & Lee 1956; White 1965; Kibblewhite 1989; Szabo & Wu 2000; Gómez Álvarez-Arenas et al.2002; Fabry et al.2003; Nicolle et al.2005; Kelly & McGough 2009; Treeby et al.2010). In this section, we will demonstrate that the generalized wave equation has a solution of attenuation that satisfies the power laws and is consistent with many laboratory measurements. We will also propose a general power-law form which is applicable to both low and high frequencies simultaneously, for any given β parameter.

Transforming wave equation (12) into the wavenumber domain leads to the following dispersion relation:

\begin{equation} k(\omega ) = \frac{\omega }{{c\sqrt {1 + \beta {{({\rm i}\omega /{\omega _0})}^\beta }} }}, \end{equation}

(26)

where k is the complex-valued wavenumber,

\begin{equation} k(\omega ) = \frac{\omega }{{v(\omega )}} - {\rm{i}}\alpha (\omega ). \end{equation}

(27)

Applying the Maclaurin expansion to eq. (26) and finding the imaginary part, according to eq. (27), the attenuation α(ω) can be obtained.

When |β(ω/ω₀)^β| ≤ 1, the attenuation can be approximated as

\begin{eqnarray} \alpha (\omega ) &\approx & \frac{{{\omega _0}\beta }}{{128\sqrt 2 c}}\bigg[ {71{{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^{1 + \beta }}\sin \frac{{\beta \pi }}{2}} - 27\beta {{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^{1 + 2\beta }}\sin (\beta \pi )\nonumber\\ && \qquad\qquad +\, 5{\beta ^2}{{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^{1 + 3\beta }}\sin \frac{{3\beta \pi }}{2} \bigg], \end{eqnarray}

(28)

which follows the power laws,

\begin{equation} \alpha (\omega ) \approx {\alpha _1}{\omega ^{1 + \beta }} + {\alpha _2}{\omega ^{1 + 2\beta }} + {\alpha _3}{\omega ^{1 + 3\beta }}. \end{equation}

(29)

Here ω ≥ 0 is assumed, as we consider causal seismic data.

One of the physical meanings of the power-law form in eq. (29) is that, for a weak viscoelastic case with a small β value, the attenuation is a linear scaling with frequency. Kibblewhite (1989) suggested that there are two mechanisms responsible for the attenuation. The primary mechanism is called ‘internal friction’ which somehow gives rise to a linear scaling with frequency, as in dry materials. The additional mechanism, due to the viscosity of the pore fluid, is responsible for any deviation from the linear power law in saturated materials.

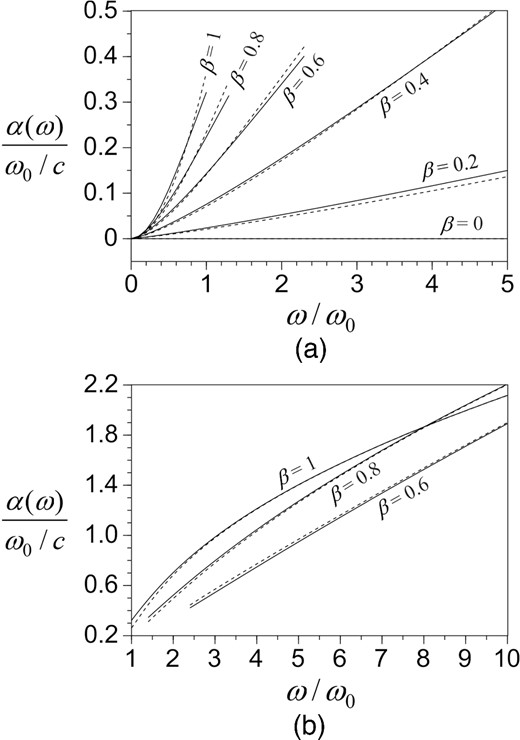
As shown in Fig. 3(a), in the case where β ≥ 0.6, the attenuation for low frequencies approaches to the (1 + β)-, (1 + 2β)- and (1 + 3β)th powers of frequency, and eq. (28) is a modification of the second power of frequency. The latter is consistent with Biot's attenuation theory at low frequencies (Biot 1956a). Fig. 3(a) indicates that this frequency-square property is valid up to ω < 2ω₀ for β = 0.6 and ω = ω₀ for 0.8 ≤ β ≤ 1.0.

Figure 3.

The attenuation follows the power law, whenever (a) |β(ω/ω0)β| ≤ 1 and (b) |β(ω/ω0)β| > 1. The solid curves are the exact solution and the dashed curves are the power-law approximation. The vertical axis is the attenuation normalized by ω0/c.

Open in new tab Download slide

The attenuation follows the power law, whenever (a) |β(ω/ω₀)^β| ≤ 1 and (b) |β(ω/ω₀)^β| > 1. The solid curves are the exact solution and the dashed curves are the power-law approximation. The vertical axis is the attenuation normalized by ω₀/c.

When |β(ω/ω₀)^β| > 1, as plotted in Fig. 3(b), the attenuation can be approximated as

\begin{eqnarray} \alpha (\omega ) &\approx & \frac{{{\omega _0}}}{c}\Bigg[ {\frac{1}{{{\beta ^{1/2}}}}{{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^{1 - \beta /2}}\sin \frac{{\beta \pi }}{4}} \nonumber\\ &&-\, \frac{1}{{2{\beta ^{3/2}}}}{{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^{1 - 3\beta /2}}\sin \frac{{3\beta \pi }}{4}\nonumber\\ &&+\, \frac{3}{{8{\beta ^{5/2}}}}{{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^{1 - 5\beta /2}}\sin \frac{{5\beta \pi }}{4}\nonumber\\ &&-\, \frac{3}{{16{\beta ^{7/2}}}}{{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^{1 - 7\beta /2}}\sin \frac{{7\beta \pi }}{4}\nonumber\\ &&+\, \frac{3}{{32{\beta ^{9/2}}}}{{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^{1 - 9\beta /2}}\sin \frac{{9\beta \pi }}{4}\nonumber\\ &&-\, \frac{1}{{256{\beta ^{11/2}}}}{{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^{1 - 11\beta /2}}\sin \frac{{11\beta \pi }}{4} \Bigg] . \end{eqnarray}

(30)

It is also in a form of power laws,

\begin{eqnarray} \alpha (\omega ) &\approx & {\alpha _{ - 1/2}}{\omega ^{1 - \beta /2}} + {\alpha _{ - 3/2}}{\omega ^{1 - 3\beta /2}} + {\alpha _{ - 5/2}}{\omega ^{1 - 5\beta /2}}\nonumber\\ &&+\, {\alpha _{ - 7/2}}{\omega ^{1 - 7\beta /2}} + {\alpha _{ - 9/2}}{\omega ^{1 - 9\beta /2}} + {\alpha _{ - 11/2}}{\omega ^{1 - 11\beta /2}}. \end{eqnarray}

(31)

This form includes Biot's attenuation theory at high frequencies (Biot 1956b): the attenuation is proportional to ω^1/2. The relationship given by eq. (31) seems much more general, being fractional powers of frequency.

Combining two scenarios, eqs (29) and (31), we propose a general form of power laws for the attenuation, as

\begin{equation} \alpha (\omega ) = \frac{{{\omega _0}}}{c}\sum\limits_n {{\lambda _n}{\beta ^n}{{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^{1 + n\beta }}} \sin \frac{{n\beta \pi }}{2}, \end{equation}

(32)

where

\begin{eqnarray} n = - \frac{{11}}{2},\quad - \frac{9}{2},\quad - \frac{7}{2},\quad - \frac{5}{2},\quad - \frac{3}{2},\quad - \frac{1}{2},\quad 1,\quad 2,\quad 3,\nonumber\\ \end{eqnarray}

(33)

and λ_n are coefficients to fit this general power-law formula to the analytical solution in eq. (21).

The series of coefficients λ_n in the power-law formula can be determined numerically, for any given β value (0 < β ≤ 1). Whenever sin (nβπ/2) = 0, for example, (β, n) = (4/5, −5/2), and (β, n) = (1, 2), we set λ_n = 0 and estimate the rest. Table 1 summarizes coefficients λ_n for the power-law form in eq. (32).

Table 1.

The coefficients in the general power-law form for the attenuation.

	λ_n (β = 0.1)	λ_n (β = 0.2)	λ_n (β = 0.3)	λ_n (β = 0.4)	λ_n (β = 0.5)
n = −11/2	0	0	−0.000042	0.000353	0.000508
n = −9/2	0.000002	0.000021	0.000465	0.004995	−0.019584
n = −7/2	−0.000013	−0.000754	−0.002632	−0.007785	−0.116293
n = −5/2	−0.000338	0.005661	0.007857	−0.003614	0.131893
n = −3/2	0.005620	0.000697	−0.006141	0.110538	−0.157434
n = −1/2	−0.010068	−0.338306	−0.075679	−0.717437	0.066795
n = 1	0.809407	−0.136882	0.325118	−0.258210	0.224411
n = 2	0.086575	−0.649135	−0.169018	0.200912	−0.056932
n = 3	−2.767400	1.170922	0.063227	−0.070068	0.008822
	λ_n (β = 0.6)	λ_n (β = 0.7)	λ_n (β = 0.8)	λ_n (β = 0.9)	λ_n (β = 1.0)
n = −11/2	0.000627	−0.000585	−0.001013	0.000335	−0.000019
n = −9/2	−0.010728	0.003230	−0.014219	−0.095917	−0.001965
n = −7/2	0.393432	−0.043753	0.034206	−0.067135	−0.042692
n = −5/2	0.264238	−0.338536	0	0.732270	0.293508
n = −3/2	−0.269011	0.318444	0.239684	0.740397	0.863421
n = −1/2	0.273594	−0.752771	−0.706726	−1.065600	−1.071839
n = 1	0.318932	0.0426558	0.043124	−0.001986	−0.001549
n = 2	−0.110450	−0.013564	−0.016306	0.000316	0
n = 3	0.047285	−0.006779	−0.001231	−0.000003	−0.000006

	λ_n (β = 0.1)	λ_n (β = 0.2)	λ_n (β = 0.3)	λ_n (β = 0.4)	λ_n (β = 0.5)
n = −11/2	0	0	−0.000042	0.000353	0.000508
n = −9/2	0.000002	0.000021	0.000465	0.004995	−0.019584
n = −7/2	−0.000013	−0.000754	−0.002632	−0.007785	−0.116293
n = −5/2	−0.000338	0.005661	0.007857	−0.003614	0.131893
n = −3/2	0.005620	0.000697	−0.006141	0.110538	−0.157434
n = −1/2	−0.010068	−0.338306	−0.075679	−0.717437	0.066795
n = 1	0.809407	−0.136882	0.325118	−0.258210	0.224411
n = 2	0.086575	−0.649135	−0.169018	0.200912	−0.056932
n = 3	−2.767400	1.170922	0.063227	−0.070068	0.008822
	λ_n (β = 0.6)	λ_n (β = 0.7)	λ_n (β = 0.8)	λ_n (β = 0.9)	λ_n (β = 1.0)
n = −11/2	0.000627	−0.000585	−0.001013	0.000335	−0.000019
n = −9/2	−0.010728	0.003230	−0.014219	−0.095917	−0.001965
n = −7/2	0.393432	−0.043753	0.034206	−0.067135	−0.042692
n = −5/2	0.264238	−0.338536	0	0.732270	0.293508
n = −3/2	−0.269011	0.318444	0.239684	0.740397	0.863421
n = −1/2	0.273594	−0.752771	−0.706726	−1.065600	−1.071839
n = 1	0.318932	0.0426558	0.043124	−0.001986	−0.001549
n = 2	−0.110450	−0.013564	−0.016306	0.000316	0
n = 3	0.047285	−0.006779	−0.001231	−0.000003	−0.000006

Open in new tab

Table 1.

The coefficients in the general power-law form for the attenuation.

	λ_n (β = 0.1)	λ_n (β = 0.2)	λ_n (β = 0.3)	λ_n (β = 0.4)	λ_n (β = 0.5)
n = −11/2	0	0	−0.000042	0.000353	0.000508
n = −9/2	0.000002	0.000021	0.000465	0.004995	−0.019584
n = −7/2	−0.000013	−0.000754	−0.002632	−0.007785	−0.116293
n = −5/2	−0.000338	0.005661	0.007857	−0.003614	0.131893
n = −3/2	0.005620	0.000697	−0.006141	0.110538	−0.157434
n = −1/2	−0.010068	−0.338306	−0.075679	−0.717437	0.066795
n = 1	0.809407	−0.136882	0.325118	−0.258210	0.224411
n = 2	0.086575	−0.649135	−0.169018	0.200912	−0.056932
n = 3	−2.767400	1.170922	0.063227	−0.070068	0.008822
	λ_n (β = 0.6)	λ_n (β = 0.7)	λ_n (β = 0.8)	λ_n (β = 0.9)	λ_n (β = 1.0)
n = −11/2	0.000627	−0.000585	−0.001013	0.000335	−0.000019
n = −9/2	−0.010728	0.003230	−0.014219	−0.095917	−0.001965
n = −7/2	0.393432	−0.043753	0.034206	−0.067135	−0.042692
n = −5/2	0.264238	−0.338536	0	0.732270	0.293508
n = −3/2	−0.269011	0.318444	0.239684	0.740397	0.863421
n = −1/2	0.273594	−0.752771	−0.706726	−1.065600	−1.071839
n = 1	0.318932	0.0426558	0.043124	−0.001986	−0.001549
n = 2	−0.110450	−0.013564	−0.016306	0.000316	0
n = 3	0.047285	−0.006779	−0.001231	−0.000003	−0.000006

	λ_n (β = 0.1)	λ_n (β = 0.2)	λ_n (β = 0.3)	λ_n (β = 0.4)	λ_n (β = 0.5)
n = −11/2	0	0	−0.000042	0.000353	0.000508
n = −9/2	0.000002	0.000021	0.000465	0.004995	−0.019584
n = −7/2	−0.000013	−0.000754	−0.002632	−0.007785	−0.116293
n = −5/2	−0.000338	0.005661	0.007857	−0.003614	0.131893
n = −3/2	0.005620	0.000697	−0.006141	0.110538	−0.157434
n = −1/2	−0.010068	−0.338306	−0.075679	−0.717437	0.066795
n = 1	0.809407	−0.136882	0.325118	−0.258210	0.224411
n = 2	0.086575	−0.649135	−0.169018	0.200912	−0.056932
n = 3	−2.767400	1.170922	0.063227	−0.070068	0.008822
	λ_n (β = 0.6)	λ_n (β = 0.7)	λ_n (β = 0.8)	λ_n (β = 0.9)	λ_n (β = 1.0)
n = −11/2	0.000627	−0.000585	−0.001013	0.000335	−0.000019
n = −9/2	−0.010728	0.003230	−0.014219	−0.095917	−0.001965
n = −7/2	0.393432	−0.043753	0.034206	−0.067135	−0.042692
n = −5/2	0.264238	−0.338536	0	0.732270	0.293508
n = −3/2	−0.269011	0.318444	0.239684	0.740397	0.863421
n = −1/2	0.273594	−0.752771	−0.706726	−1.065600	−1.071839
n = 1	0.318932	0.0426558	0.043124	−0.001986	−0.001549
n = 2	−0.110450	−0.013564	−0.016306	0.000316	0
n = 3	0.047285	−0.006779	−0.001231	−0.000003	−0.000006

Open in new tab

Table 1 lists the nine coefficients for each case with a constant β value. Because those additive terms in eq. (32) are not orthogonal to each other, using more or less terms in curve fitting will alter the estimated coefficients listed in the table. The 9-term generalized power-law formula in eq. (32) can fit both low and high frequencies with sufficient accuracy. This is certainly an advantage over any conventional analysis conducted over separated regimes (Holm & Näsholm, 2011, 2014).

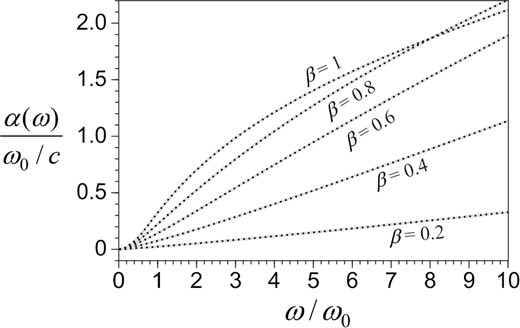
In Table 1, the coefficients are estimated from an individual attenuation curve of a single β constant. If different attenuation curves corresponding to different β values are combined into a single group for the coefficient evaluation, it will severely compromize the accuracy of curve fitting. Each group of coefficients is fitted to a wide range of frequency variation, up to 10 times the reference frequency ω₀. In Fig. 4, power-law (black dotted) attenuation curves are overlaid with the (grey solid) curves of the analytical attenuation. The rms error for each case is <0.0015.

Figure 4.

Open in new tab Download slide

The analytical solutions of the attenuation are fitted by the power law. The grey solid curves are the analytical solutions and the black dotted curves are the power-law approximations. They match each other perfectly.

The wave dynamic properties (the attenuation and phase velocity) can be related to the mechanical properties (permeability, grain size, density and porosity) of a sediment (Hovem and Ingram 1979; Buckingham 1997). These power-law functions will be very useful for extrapolating laboratory measurements from an intermediate–high frequency range to a low-frequency range.

CONCLUSIONS

This paper has proposed a generalized wave equation which covers the viscoelastic case and the pure elastic case in a single equation. The parameter (β) controlling the degree of viscoelasticity also balances the characteristics between the elasticity and the viscoelasticity of the subsurface media. The analytical solution of the generalized wave equation is expressed explicitly in terms of the attenuation and the velocity dispersion.

This paper has also proved that the attenuation component of the generalized wave equation, defined by any constant β parameter, satisfies the power law of frequency. Since the power-law form is a general physical observation of the attenuation depending on the frequency, this generalized wave equation can well represent wave propagation in subsurface media. The theoretical solution might lead to a generalized definition of seismic wavelets (Wang 2015).

The author is grateful to the National Natural Science Foundation of China (Grant No. 41474111), and the sponsors of the Centre for Reservoir Geophysics, Imperial College London, for supporting this research.

REFERENCES

Bagley

R.

Torvik

P.

A theoretical basis for the application of fractional calculus to viscoelasticity

J. Rheol.

1983

27

201

210

Month:	Total Views:
December 2016	1
January 2017	2
February 2017	5
March 2017	12
April 2017	10
May 2017	10
June 2017	16
July 2017	9
August 2017	5
September 2017	9
October 2017	12
November 2017	16
December 2017	1
January 2018	3
February 2018	13
March 2018	9
April 2018	7
May 2018	7
June 2018	6
July 2018	24
August 2018	5
September 2018	7
October 2018	20
November 2018	7
December 2018	9
January 2019	11
February 2019	21
March 2019	51
April 2019	31
May 2019	29
June 2019	30
July 2019	55
August 2019	42
September 2019	48
October 2019	57
November 2019	40
December 2019	17
January 2020	67
February 2020	32
March 2020	45

Article Contents

Generalized viscoelastic wave equation

Abstract

INTRODUCTION

GENERALIZED WAVE EQUATION

Unified elastic-viscoelastic model

The combining factor

The wave equation

THE ANALYTICAL SOLUTION

POWER LAWS FOR THE ATTENUATION

CONCLUSIONS

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only